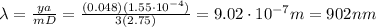Answer:
902 nm
Step-by-step explanation:
We can solve the problem by using the formula for the diffraction from double slit:
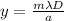
where:
y is the distance of the m-th order diffraction maximum from the central fringe
 is the wavelength of the light used
is the wavelength of the light used
D is the distance of the screen from the slits
a is the distance between the slits
In this situation, we know:
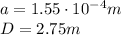
And also,
y = 0.048 m for m = 3 (third order bright fringe)
Solving the equation for
 , we find the wavelength:
, we find the wavelength: