Question

A baseball team plays in a stadium that holds 62000 spectators. With the ticket price at $11, the average attendance has been 27000. When the price dropped to $8, the average attendance rose to 31000. Assume that attendance is linearly related to the ticket price.

What ticket price would maximize revenue?

Answer 1

$15.625

Explanation:

Let the revenue collected be R and price per spectator be p then the number of spectators be N. Therefore

R=Np

Using equation of slope of y=mx +c where m is gradient and c is y-intercept

When p=$11, N=27000 and when p=$8, N=31000

The gradient, m will be

`m=\frac {31000-27000}{8-11}= -1333.33`

To get the y-intercept

N=-1333.33p+c

When spectator number n is 27000, the price p is $11

27000=-1333.33(11)+c hence we solve c

c=27000+(11*1333.33)= 41666.67

Therefore, the linear equation is

N=-1333.33p+ 41666.67

Substituting the linear equation into R=Np we obtain

R=p(-1333.33p+41666.67)

`R=-1333.33p^(2)+41666.67p`

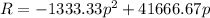
To obtain maximum revenue, we differentiate the above with respect to price hence obtain

0=2*-1333.33p+41666.67

`p=-\frac {41666.67}{2(-1333.33)}= 15.625`

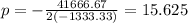
Therefore, the price that maximizes revenue is $15.625