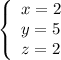Question

A company produces 3 types of widgets. On a given day, the company was able to produce 9 total widgets (combining all 3 types). Widget A costs $3 to produce, Widget B costs #2 to produce, and Widget C costs $1 to produce. The cost to produce the widgets each day is $18. The company produces one more Widget B than the sum of the Widgets A & C. How many of each type of Widget is produced?

Set up three equations with three variables. Then,use a matrix to solve for the number of each type of widget.

Answer 1

2 widgets A, 5 widgets B and 2 widgets C

Explanation:

Let

• x be the number of widgets A;
• y be the number of widgets B;
• z be the number of widgets C.

1. On a given day, the company was able to produce 9 total widgets, then

`x+y+z=9`

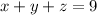
2. The company produces one more Widget B than the sum of the Widgets A & C, then

`y=x+z+1\\ \\x-y+z=-1`

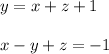
3. Widget A costs $3 to produce, so x widgets A cost $3x.

Widget B costs $2 to produce, so y widgets B cost $2y.

Widget C costs $1 to produce, so z widgets C cost $z.

The cost to produce the widgets each day is $18, thus

`3x+2y+z=18`

4. We get the system of three equations:

`\left\{\begin{array}{l}x+y+z=9\\x-y+z=-1\\3x+2y+z=18\end{array}\right.`

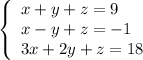
Write an augmented matrix for this system

`\left(\begin{array}{ccccc}1&1&1&|&9\\1&-1&1&|&-1\\3&2&1&|&18\end{array}\right)\sim \left(\begin{array}{ccccc}1&1&1&|&9\\0&2&0&|&10\\0&1&2&|&9\end{array}\right)\sim \left(\begin{array}{ccccc}1&1&1&|&9\\0&2&0&|&10\\0&0&4&|&8\end{array}\right)`

Therefore,

`\left\{\begin{array}{l}x+y+z=9\\2y=10\\4z=8\end{array}\right.`

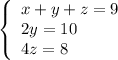
Hence

`\left\{\begin{array}{l}x=2\\y=5\\z=2\end{array}\right.`