Question

In 1955, a magazine reported that women worked, on average, 80 hours per week. Recently, research has been investigating whether or not the women’s movement has, in fact, been accompanied by an increase in the average work week for women (combining employment outside the home and work in the home). The population standard deviation is known to be 12 hours. Suppose a college student conducts a study to determine if the mean work week has increased, randomly sampling 80 women. The sample mean was 83 hours per week with a sample standard deviation of 10.Does it appear that the mean work week has increased for women at the 5% level?

Answer 1

Answer with explanation:

Let
`\mu` be the population mean.

As per given we have,

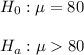`H_0:\mu=80\\\\ H_a:\mu>80` , since alternative hypothesis is right tailed , so the test is a right-tailed test.

Test statistic :
`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

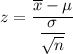
For, n=80
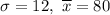`\sigma=12,\ \overline{x}=80` , we have

`z=(83-80)/((12)/(√(80)))\approx2.236`

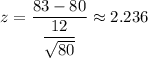
Critical z-value at
`\alpha=0.05` =1.645

Since the test statistic value is greater than the critical z-value, so we reject the null hypothesis, i.e. alternative hypothesis is accepted.

Conclusion: We have enough evidence to support the claim that the mean work week has increased for women at the 5% level.