Question

A ladder is slipping down a vertical wall. If the ladder is 10 ft long and the top of it is slipping at the constant rate of 4 ​ft/s, how fast is the bottom of the ladder moving along the ground when the bottom is 8 ft from the​ wall? Round to the nearest tenth.

Answer 1

Speed will be: 1.33ft/s

Step-by-step explanation:

If ladder is 10 ft long and bottom is 8 ft from the wall then by Pythagoras theorem we can find the height of the wall where ladder touches. (before it started slipping)

`10^2 = 8^2 + x^2`

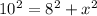
thus
`x^2 = 100 - 64 = 36`

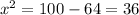
Giving x= 6 ft. If the ladder is falling with a speed of 4ft/s it will take 1.5 seconds to cover the 6ft distance.

This shows that the bottom of ladder will travel from 8ft to 10 ft in 1.5 seconds. Thus covering 2 ft in 1.5 seconds making the speed to be:

v = S / t

v = 2 / 1.5

v = 1.33 ft/s