Answer: lower bound = 21%
upper bound = 31%
Explanation:
Let
 be the sample proportion.
be the sample proportion.
As per given we have,
sample size : n=675
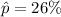
The maximum margin of sampling error with 95% confidence : E=±5%
We know that confidence interval is given by :-
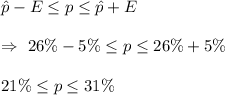
The 95% confidence interval for the percent of all coffee drinkers who would say they are addicted to coffee :-
lower bound = 21%
upper bound = 31%