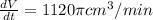Question

the radius ???? of a sphere is expanding at a rate of 70 cm/min. The volume of a sphere is ????=43????????3 and its surface area is 4????????2. Determine the rate at which the volume is changing with respect to time at ????=2 min, assuming that ????=0 at ????=0.

Answer 1

`(dV)/(dt)=1120 \pi cm^3/min`

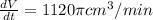
Explanation:

We are given that

Radius of sphere expanding at the rate=
`(dr)/(dt)=70 cm/min`

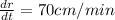
Volume of sphere=
`V=(4)/(3)\pi r^3`

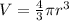
Surface area of sphere=
`S=4\pi r^2`

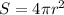
We have to determine the rate at which the volume is changing with respect to time at r= 2 cm.

`V=(4)/(3)\pi r^3`

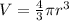
Differentiate w.r.t time

`(dV)/(dt)=4\pi r^2(dr)/(dt)`

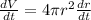
Substitute the values then we get

`(dV)/(dt)=4\pi (2)^2(70)=1120 \pi cm^3/min`

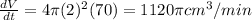
Hence, the rate at which the volume of sphere is changing is given by

`(dV)/(dt)=1120 \pi cm^3/min`