Answer:
(a) Co-ordinate rule is
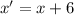 and
and

(b) Co-ordinates of B' and C' are
 and
and
 respectively.
respectively.
Explanation:
(a)
Here, the co-ordinates of A
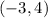 are translated to A'
are translated to A'
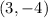 .
.
For the co-ordinates A and A',
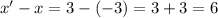 and
and
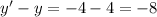
So, x value of A has shifted to right by 6 units and y value of A has shifted 8 units down.
Hence, the co-ordinate rule that maps ΔABC onto ΔA'B'C' is:
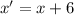 and
and
 .
.
(b)
Using the co-ordinate rule, we can find the co-ordinates of B' and C'.
For B,
 and
and
 .
.
So,
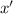 of B' is
of B' is
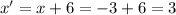
And,
 of B' is
of B' is
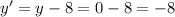 .
.
Therefore, co-ordinates of B' are
 .
.
For C,
 and
and
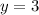 .
.
So,
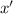 of C' is
of C' is
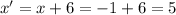
And,
 of C' is
of C' is
 .
.
Therefore, co-ordinates of C' are
 .
.