Answer:
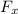 = -12 N ,
= -12 N ,
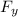 = -80 N and
= -80 N and
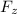 = - 44 N
= - 44 N
Step-by-step explanation:
The force is related to the potential energy by the formula
F = -Δ U = - (
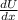 i ^ +
i ^ +
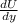 j ^ +
j ^ +
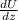 k ^)
k ^)
It indicates the potential energy
U = 2xyz + 3z² + 4yx + 16
To solve this problem let's make the derivatives, to find each component of the force
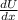 = 2yz + 0 + 4y + 0 = 2yz + 4y
= 2yz + 0 + 4y + 0 = 2yz + 4y
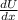 = 2xz + 0 + 4x + 0 = 2xz + 4x
= 2xz + 0 + 4x + 0 = 2xz + 4x
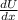 = 2xy + 3 2z + 0 +0 = 2xy + 6z
= 2xy + 3 2z + 0 +0 = 2xy + 6z
We look for the expression for the force in each axis
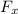 = - 2yz - 4y
= - 2yz - 4y
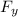 = -2xz -4x
= -2xz -4x
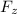 = -2xy -6z
= -2xy -6z
We calculate at the point P = (20 i ^ + 1j ^ + 4 k ^) m
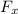 = - 2 1 4 - 4 1
= - 2 1 4 - 4 1
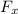 = -12 N
= -12 N
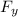 = - 2 20 4 - 4 20
= - 2 20 4 - 4 20
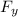 = -80 N
= -80 N
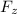 = - 20 1 - 6 4
= - 20 1 - 6 4
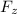 = - 44 N
= - 44 N
We put together the expression for strength
F = (-12 i ^ - 80j ^ -44k ^) N