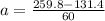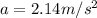Question

"You’re pulling a crate with a mass of 60 kg along a level floor with a rope that’s inclined at an angle = 30above the horizontal. Assume that between the floor and the crate the coefficient of static friction is 0.40 and the coefficient of kinetic friction is 0.30. The tension in the rope is measured to be 300 N."

Answer 1

`a = 2.14 m/s^2`

Step-by-step explanation:

Tension force in the rope is given as

`T = 300 N`

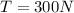
now the rope is inclined at an angle of 30 degree above the horizontal

so the two components of the tension force is given as

`F_x = Tcos30`

`F_x = 300 cos30 = 259.8 N`

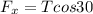
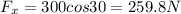
also in vertical direction we have

`F_y = T sin30`

`F_y = 300 sin30 = 150 N`

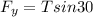
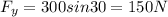
now we will say that normal force by the ground is given as

`F_n + F_y = mg`

`F_n + 150 = (60 * 9.8)`

`F_n = 438 N`

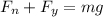
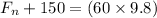
now the maximum static friction on the crate is given as

`F_s = \mu_s F_n`

`F_s = 0.40(438)`

`F_s = 175.2 N`

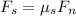
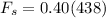
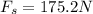
also we can find the kinetic friction as

`F_k = \mu_k F_n`

`F_k = 0.30 (438)`

`F_k = 131.4 N`

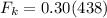
since horizontal applied force is more than the maximum static friction so here the frictional force on the crate must be kinetic friction

and the acceleration of the crate is given as

`F_x - F_k = ma`

`259.8 - 131.4 = 60 a`

`a = (259.8 - 131.4)/(60)`

`a = 2.14 m/s^2`