Answer:
a) 75.34%
b) 13.53%
Explanation:
First, let us consider the cumulative exponential distribution
![F(t) = P[T\leq t] = 1 - e^(-rt)](https://img.qammunity.org/2020/formulas/mathematics/college/hmcgj9t0man86b75ozuwc7usp6hnqelnyh.png)
Where
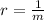 and m denotes the mean
and m denotes the mean
Therefore, our cumulative distribution for this exercise is as it follows:
![P[T\leq t] = 1-e^{-(1)/(15)t }](https://img.qammunity.org/2020/formulas/mathematics/college/itx5z8ltb1f6wupw4wfoxwmsnnvj122syr.png)
a) According to the distribution, the first question can be calculated as it follows:
![P[T\leq 21]=1-e^{-(1)/(15)*21 } =1-e^{-(7)/(5) }](https://img.qammunity.org/2020/formulas/mathematics/college/ihr6u8hn71x4881v0k84xqz8azoyn5ooeb.png)
![P[T\leq 21]=0.7534](https://img.qammunity.org/2020/formulas/mathematics/college/u47mj3xyakxkgq95locjcoch0fh9cwp8wx.png)
Hence, the probability that the piece will break down in the next 21 days is 75.34%
b) Now, take into account that we now need the probability complement for applying the cumulative distribution like this:
![P[T\geq 30]=1-P[T<30]](https://img.qammunity.org/2020/formulas/mathematics/college/j8pc0j2il95k67hm9zmixhelfp2sepla9o.png)
![P[T\geq 30]=1-(1-e^{-(1)/(15)*30 })=e^(-2)](https://img.qammunity.org/2020/formulas/mathematics/college/4xxlweuk2gkbhmiaoq9scrg60k52vg7frs.png)
![P[T\geq 30]=0.1353](https://img.qammunity.org/2020/formulas/mathematics/college/zb9vfyldr3a4jc7qph3fkawhcepgsck0u0.png)
Therefore, we have that the probability that the generator will operate for 30 days without a breakdown is 13.53%