Answer: -0.87
Explanation:
As per given , we have
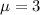
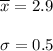
Sample size : n= 19
Test statistic :
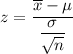
By substituting the corresponding values , we get
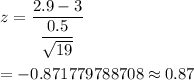 [Rounded to the nearest two decimal places.]
[Rounded to the nearest two decimal places.]
Hence, the test statistic (z-score) of this one-mean hypothesis test= -0.87