Question

The length of a standard jewel case is 7cm more than its width. The area of the rectangular top of the case is 294 cm^2. Find the length and width of the jewel case.

Answer 1

Length = 21 cm

Width = 14 cm

Explanation:

Let the width of the jewel case = m cm

So, the length of the case = (m + 7) cm

Area of the case =
`294cm^(2)`

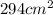
Now, Area of a Rectangle = Length x Width

= m x (m + 7)

⇒ m x (m + 7) = 294

or,
`m^(2)  + 7m - 294 = 0`

⇒
`m^(2)  + 21m  - 14m - 294 = 0`

or,
`m(m+21) -14( m + 21)`

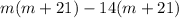
⇒(m + 21)(m -14) = 0

Hence, either (m + 21) = 0 ⇒ m = -21

or, (m -14) = 0⇒ m = 14

Since, m is the width of a case, so it can not be negative

Hence the width of the jewel case = m = 14 cm

And the length of the case = (m + 7) = 14 + 7 = 21 cm