Question

In the electric currect​ flow, it is found that the resistance​ (measured in the units called​ ohms) offered by a fixed length of wire of a given material varies inversely as the square of the diameter of the wire. If a wire 0.01 in. in diameter has a resistance of 0.447 ​ohms, what is the resistance of a wire of the same length and material with diameter 0.0192 in. to the nearest​ ten-thousandth?

Answer 1

0.1213 ohms

Explanation:

If a quantity, A, varies inversely as the square of another quantity, B, we can write the proportionality equation as:

`A=(k)/(B^2)`

In our problem, we have,

Resistance varies inversely as the square of Diameter

Let resistance be r and diameter be d, so we can write:

`r=(k)/(d^2)`

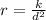
Where

k is the proportionality constant to be found

Now, it is given that

r = 0.447

d = 0.01

We substitute and find k:

`r=(k)/(d^2)\\0.447=(k)/(0.01^2)\\0.447=(k)/(0.0001)\\k=0.0001*0.447\\k=0.0000447`

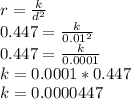
Again, we need to solve for r, given k = 0.0000447 and now d = 0.0192. Thus, we have:

`r=(k)/(d^2)\\r=(0.0000447)/(0.0192^2)\\r=0.1213`

The resistance is 0.1213 ohms