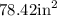2 Answers

Bertrand Le Roy · Answer 1 · 2020-05-30T03:38:50+0000

Answer:

The area of parallelogram ABCD is
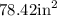
$78.42 \mathrm{in}^(2)$

Explanation:

Given:

AD = 12 in

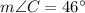
$m \angle C=46^(\circ)$

$m \angle D B A=72^(\circ)$

To Find:

The area of parallelogram ABCD=?

Solution:

When we construct the parallelogram with the given data, we get a parallelogram formed by 12 cm as one side and an angle with 46 degrees.

The area of the parallelogram can be calculated by
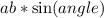
$a b * \sin (a n g l e)$

Substituting the value of a=12 we have

$\text { Area of parallelogram }=12 * \text { bsin } 46$

To find the value of b,

We know that area of a triangle can be expressed as,

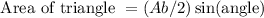
$\text { Area of triangle }=(A b / 2) \sin (\text {angle})$

So,

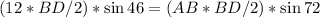
$(12 * B D / 2) * \sin 46=(A B * B D / 2) * \sin 72$

Cancelling BD and 2 on both sides we get,

$12 * \sin 46=A B * \sin 72$

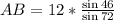
$A B=12 * (\sin 46)/(\sin 72)$

Therefore,

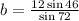
$b=(12 \sin 46)/(\sin 72)$

Substituting the value of b,

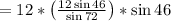
$=12 *\left((12 \sin 46)/(\sin 72)\right) * \sin 46$

=78.42

So the area of the parallelogram is
$78.42 \mathrm{in}^(2)$

Please log in or register to add a comment.