Answer:
395,925,972 or 396 million
Explanation:
Since the population growth rate is 3.5 annual that implies that the increase in population has to be recalculated at the end of each year (i.e. it is not a constant amount like a 100 people or a 1000 people but it changes every year)
To solve this problem we will use the following equation
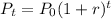
Where
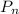 is population at year 't'
is population at year 't'
 is initial population i.e. 100 million
is initial population i.e. 100 million
 is growth rate is a fraction i.e. 3.5/100
is growth rate is a fraction i.e. 3.5/100
 is years passed i.e. 40
is years passed i.e. 40
Now all we have to do is plugin the values
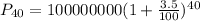
The answer is 395,925,972