Answer:
a) 2¹³
b) 0.0873
c) 0.9983
d) 0.9538
Explanation:
a) How many different outcomes are possible?
For every toss, there are two possible outcomes (heads or tails), so if we toss the coin 13 times the total of outcomes possible is 2¹³
b) What is the probability of getting exactly 4 heads?
The definition of probability is an event is: number of favourable events/ number of total events.
When we have two possible outcomes p, q and we repeat the experiment multiple times, we apply the Binomial distribution, in this distribution the probability of getting exactly k successes in n trials is given by
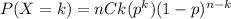 where p represents the probability of success. nCk refers to the combinations of k elements out of n elements.
where p represents the probability of success. nCk refers to the combinations of k elements out of n elements.
So we have to know how many different ways we can get exactly 4 heads.
let's name p = probability of getting heads = 0.5
1 -p = probability of getting tails = 0.5
We are going to toss the coin 13 different times and we want to get heads 4 times and tails 9 times.
So, by the Binomial Distribution we would have:
P(X=4) = 13C4 (0.5)⁴(0.5)⁹ = 715 (0.5)¹³ = 0.0873
Thus, the probability of getting exactly 4 heads is 0.0873.
c) What is the probability of getting at least 2 heads?
We are going to use the same binomial distribution but now we need at least to heads, this can be written as 1 - (P(X=0) + P(X=1))
P(X=0) + P(X=1) = 13C0 (0.5)⁰(0.5)¹³ + 13C1 (0.5)¹(0.5)¹² = 0.0001220703125 + 0.0015869140625 = 0.001708984375
1 - 0.001708984375 = 0.998291015625
The probability of getting at least 2 heads is 0.9983
d) What is the probability of getting at most 9 heads?
We are going to use the same binomial distribution but now we need at most 9 heads. This can be written as 1 - (P(X=10) + P(X = 11) + P(X=12) + P(X=13))
1 - (P(X=10) + P(X = 11) + P(X=12) + P(X=13)) =1 -(13C10(0.5)¹⁰(0.5)³ + 13C11(0.5)¹¹(0.5)²+ 13C12(0.5)¹²(0.5)¹ + 13C13(0.5)¹³(0.5)⁰) = 0.95385742188
The probability of getting at most 9 heads is 0.9538