Question

A test indicates the presence of a particular dis- ease 90% of the time when the disease is present and the presence of the disease 2% of the time when the disease is not present. If 0.5% of the population has the disease, cal- culate the conditional probability that a person selected at random has the disease if the test indicates the presence of the disease.

Answer 1

Explanation:

We have these following probabilities:

A 0.5% probability that a person has the disease.

A 99.5% probability that a person does not have the disease.

If a person has the disease, a 90% probability that the test indicates the disease.

If a person does not have the disease, a 2% probability that the test indicates the disease.

Calculate the conditional probability that a person selected at random has the disease if the test indicates the presence of the disease.

This can be formulated as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula

`P = (P(B).P(A/B))/(P(A))`

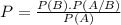
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

So:

What is the probability of the person having the disease, given that the test indicated the presence of the disease?

P(B) is the probability of the person having the disease. So
`P(B) = 0.005`.

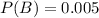P(A/B) is the probability of the person being diagnosticated, given that she has the disease. So
`P(A/B) = 0.90`.

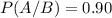P(A) is the probability of the person being diagnosticated. That is 90% of 0.5% and 2% of 99.5%. So

`P(A) = 0.005(0.90) + 0.02(0.995) = 0.0244`

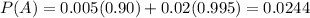
Finally

`P = (P(B).P(A/B))/(P(A))`

`P = (0.005*0.90)/(0.0244)`

`P = 0.1844`.

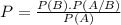
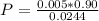
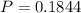If the test indicates the presence of the disease, there is a 18.44% probability that the person has the disease.