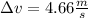Question

A 81 kg man is riding on a 40 kg cart traveling at a speed of 2.3 m/s. He jumps off with zero horizontal speed relative to the ground. What is the resulting change in the cart's speed, including sign?

Answer 1

`\Delta v= 4.66(m)/(s)`

Step-by-step explanation:

In this case we have to use the Principle of conservation of Momentum:

This principle says that in a system the total momentum is constant if no external forces act in the system. The formula is:

`m_1v_1+m_2v_2=m_1u_1+m_2u_2`

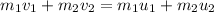
Where:

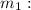`m_1:` Mass of the first object.

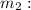`m_2:` Mass of the second object.

`v_1:` Initial velocity of the first object.

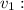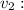`v_2:` Initial velocity of the second object.

`u_1:` Final velocity of the first object.

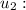`u_2:` Final velocity of the second object.

In this problem we have:

`m_1=81kg\\m_2=40kg\\v_1_2=2.3(m)/(s)`

`u_1=0(m)/(s)`

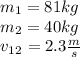
Observation:
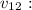`v_1_2:` Is because the system has the same initial velocity.

First we have to find
`u_2`,

`m_1v_1+m_2v_2=m_1u_1+m_2u_2`

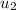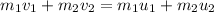
We can rewrite it as:

`(m_1+m_2)v_1_2=m_1u_1+m_2u_2`

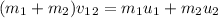
Replacing with the data:

`(m_1+m_2)v_1_2=m_1u_1+m_2u_2\\\\(81kg+40kg)2.3(m)/(s)=81kg(0(m)/(s))+40kg(u_2)\\\\(121kg)2.3(m)/(s)=40kg(u_2)\\\\((121kg)2.3(m)/(s))/(40kg)=u_2\\\\(278.3)/(40)(m)/(s)=u_2\\\\6.96(m)/(s)=u_2`

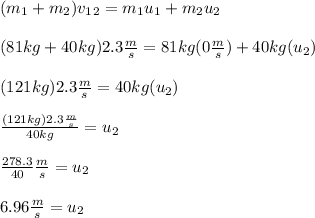
We found the final velocity of the cart, but the problem asks for the resulting change in the cart speed, this means:

`\Delta v=u_2-v_2\\\Delta v=6.96(m)/(s)-2.3(m)/(s)\\\Delta v= 4.66(m)/(s)`

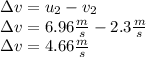
Then, the resulting change in the cart speed is:

`\Delta v= 4.66(m)/(s)`