Answer:
This means that there is a 1-0.3594 = 0.6406 = 64.06% probability that the elevator is overloaded. This a good chance that the elevator's limit weight will be exceeded. So, this elevator does not appear to be safe.
Explanation:
Problems of normally distributed samples can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by
, the zscore of a measure X is given by

After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X. Subtracting 1 by the pvalue, we This p-value is the probability that the value of the measure is greater than X.
In this problem, we have that:
Assume that weights of males are normally distributed with a mean of 163 lb and a standard deviation of 29 lb.
This means that
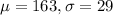 .
.
We have a sample of 12 adults, and we want to calculate the zscore of THE SAMPLE'S AVERAGE so we need to find the standard deviation of the sample. This is
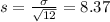
Find the probability that it is overloaded because they have a mean weight greater than 160.
This is 1 subtracted by the pvalue of Z when
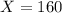

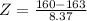

 has a pvalue of 0.3594.
has a pvalue of 0.3594.
This means that there is a 1-0.3594 = 0.6406 = 64.06% probability that the elevator is overloaded. This a good chance that the elevator's limit weight will be exceeded. So, this elevator does not appear to be safe.