Question

Intellectual development (Perry) scores were determined for 21 students in a first-year, project-based design course. (Recall that a Perry score of 1 indicates the lowest level of intellectual development, and a Perry score of 5 indicates the highest level.) The average Perry score for the 21 students was 3.27 and the standard deviation was .40. Apply the confidence interval method of this section to estimate the true mean Perry score of all undergraduate engineering students with 99% confidence. Interpret the results.

Answer 1

The 99% confidence interval is (3.0493, 3.4907).

We are 99% sure that the true mean of the students Perry score is in the above interval.

Explanation:

Our sample size is 21.

The first step to solve this problem is finding our degrees of freedom, that is, the sample size subtracted by 1. So

`df = 21-1 = 20`.

Then, we need to subtract one by the confidence level
`\alpha` and divide by 2. So:

`(1-0.99)/(2) = (0.01)/(2) = 0.005`

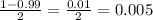
Now, we need our answers from both steps above to find a value T in the t-distribution table. So, with 20 and 0.005 in the two-sided t-distribution table, we have
`T = 2.528`

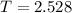
Now, we find the standard deviation of the sample. This is the division of the standard deviation by the square root of the sample size. So

`s = (0.40)/(√(21)) = 0.0873`

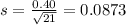
Now, we multiply T and s

`M = 2.528*0.0873 = 0.2207`

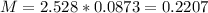
Then

The lower end of the interval is the mean subtracted by M. So:

`L = 3.27 - 0.2207 = 3.0493`

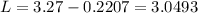
The upper end of the interval is the mean added to M. So:

`LCL = 3.27 + 0.2207 = 3.4907`

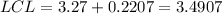
The 99% confidence interval is (3.0493, 3.4907).

Interpretation:

We are 99% sure that the true mean of the students Perry score is in the above interval.