Question

For a certain river, suppose the drought length Y is the number of consecutive time intervals in which the water supply remains below a critical value y0 (a deficit), preceded by and followed by periods in which the supply exceeds this critical value (a surplus). An article proposes a geometric distribution with p = 0.383 for this random variable. (Round your answers to three decimal places.) (a) What is the probability that a drought lasts exactly 3 intervals? At most 3 intervals? exactly 3 intervals at most 3 intervals. (b) What is the probability that the length of a drought exceeds its mean value by at least one standard deviation?

Answer 1

a) There is a 9% probability that a drought lasts exactly 3 intervals.

There is an 85.5% probability that a drought lasts at most 3 intervals.

b)There is a 14.5% probability that the length of a drought exceeds its mean value by at least one standard deviation

Explanation:

The geometric distribution is the number of failures expected before you get a success in a series of Bernoulli trials.

It has the following probability density formula:

`f(x) = (1-p)^(x)p`

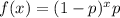
In which p is the probability of a success.

The mean of the geometric distribution is given by the following formula:

`\mu = (1-p)/(p)`

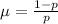
The standard deviation of the geometric distribution is given by the following formula:

`\sigma = \sqrt{(1-p)/(p^(2))`

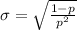
In this problem, we have that:

`p = 0.383`

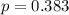
So

`\mu = (1-p)/(p) = (1-0.383)/(0.383) = 1.61`

`\sigma = \sqrt{(1-p)/(p^(2))} = \sqrt{(1-0.383)/((0.383)^(2))} = 2.05`

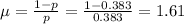
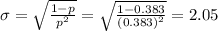
(a) What is the probability that a drought lasts exactly 3 intervals?

This is
`f(3)`

`f(x) = (1-p)^(x)p`

`f(3) = (1-0.383)^(3)*(0.383)`

`f(3) = 0.09`

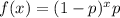
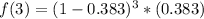
There is a 9% probability that a drought lasts exactly 3 intervals.

At most 3 intervals?

This is
`P = f(0) + f(1) + f(2) + f(3)`

`f(x) = (1-p)^(x)p`

`f(0) = (1-0.383)^(0)*(0.383) = 0.383`

`f(1) = (1-0.383)^(1)*(0.383) = 0.236`

`f(2) = (1-0.383)^(2)*(0.383) = 0.146`

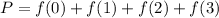
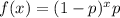
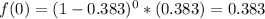
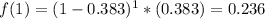
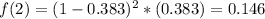
Previously in this exercise, we found that
`f(3) = 0.09`

So

`P = f(0) + f(1) + f(2) + f(3) = 0.383 + 0.236 + 0.146 + 0.09 = 0.855`

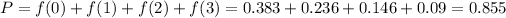
There is an 85.5% probability that a drought lasts at most 3 intervals.

(b) What is the probability that the length of a drought exceeds its mean value by at least one standard deviation?

This is
`P(X \geq \mu+\sigma) = P(X \geq 1.61 + 2.05) = P(X \geq 3.66) = P(X \geq 4)`.

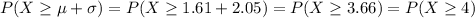We are working with discrete data, so 3.66 is rounded up to 4.

Either a drought lasts at least four months, or it lasts at most thee. In a), we found that the probability that it lasts at most 3 months is 0.855. The sum of these probabilities is decimal 1. So:

`P(X \leq 3) + P(X \geq 4) = 1`

`0.855 + P(X \geq 4) = 1`

`P(X \geq 4) = 0.145`

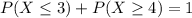
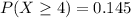
There is a 14.5% probability that the length of a drought exceeds its mean value by at least one standard deviation