Missing details in the question:
The velocities before collision are
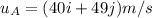

After the collision:
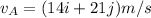
(a) 61 m/s
We can solve the problem by simply treating separately the x- and the y-components of the motion.
Here we want to analzye the motion along x. We have:
 is the initial velocity of A along the x-direction
is the initial velocity of A along the x-direction
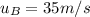 is the initial velocity of B along the x-direction
is the initial velocity of B along the x-direction
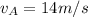 is the final velocity of A along the x-direction
is the final velocity of A along the x-direction
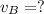 is the final velocity of B along the x-direction
is the final velocity of B along the x-direction
Since the total momentum along the x-direction must be conserved, we can write
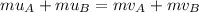
where
m = 2.3 kg is the mass of the two bodies. Since the mass is the same, we can eliminate it from the equation,
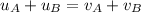
And so, we find the final velocity of B along the x-direction:
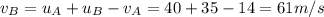
(b) 39 m/s
Similarly to what we did in part a), here we analyze the conservation of momentum along the y-direction.
We have:
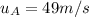 is the initial velocity of A along the y-direction
is the initial velocity of A along the y-direction
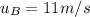 is the initial velocity of B along the y-direction
is the initial velocity of B along the y-direction
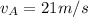 is the final velocity of A along the y-direction
is the final velocity of A along the y-direction
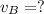 is the final velocity of B along the y-direction
is the final velocity of B along the y-direction
Since the total momentum along the y-direction must be conserved, we can write
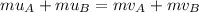
Since the mass is the same, we can eliminate it from the equation,
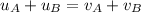
And so, we find the final velocity of B along the y-direction:
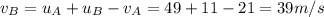
c) +615 J
Here we have to find the total kinetic energy before and after the collision first.
First, we have to find the speed of each object before and after the collision. We have:
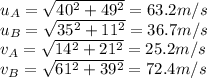
So, the total kinetic energy before the collision was
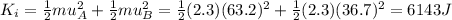
While after the collision
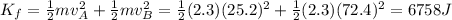
So, the change in kinetic energy is
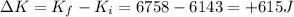
(note that the system cannot gain kinetic energy in the collision, unless there is an external force acting on it)