Answer:
F₃ is 2.83 N at 45° south of west.
Step-by-step explanation:
A force, F₁, of magnitude 2.0 N and directed due east is exerted on an object. A second force exerted on the object is F₂ = 2.0 N, due north.
Considering east as positive x direction and north as positive y direction.
F₁ = 2 i
F₂ = 2 j
First let us find the resultant of F₁ and F₂
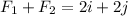
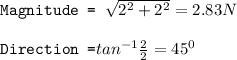
Hence the resultant is 2.83 N at 45° north of east.
For F₃ to cancel the resultant it should be opposite to the direction of the resultant and it should have same magnitude.
So F₃ is 2.83 N at 45° south of west.