Answer: a) 0.637
d) 0.04397
Explanation:
The formula to calculate the expected value and standard error for proportion (p) is given by :-

 , where n is the sample size.
, where n is the sample size.
Given : The BLS reported in February 2012 that the labor force participation rate in the United States was 63.7% .
i.e. the proportion of labor force participation rate in the United States : p=0.637
A marketing company asks 120 working-age people if they either have a job or are looking for a job, or, in other words, whether they are in the labor force.
i.e. n= 120
Then, the expected value and the standard error for a labor participation rate in the company’s sample will be :-
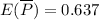

Hence, the correct answers are : a) 0.637 (For expected value)
d) 0.04397 (For standard error .)