Question

One measure of general health is your body mass index (BMI). Adults with a BMI between 18.5 and 24.9 are generally considered to have an ideal body weight for their height. The mean BMI for adults in a certain country is 24.6. Suppose the BMI for adults in this country is normally distributed with standard deviation 1.2. (Round your answers to four decimal places.) Suppose one adult from this country is selected at random. What is the probability that the person's BMI is more than 25.5?

Answer 1

Answer: 0.2266

Explanation:

Let x represents the the BMI for adults .

As we consider the given description, we have

`\mu=24.6,\ \sigma=1.2`

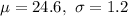
We assume that the BMI for adults in this country is normally distributed with standard deviation 1.2.

Then, z-value for x=25.5 will be:-

`z=(x-\mu)/(\sigma)=(25.5-24.6)/(1.2)=0.75`

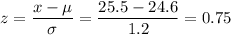
P-value :
`P(x>25.5)=P(z>0.75)=1-P(z<0.75)`

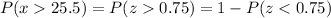
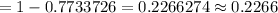`=1-0.7733726=0.2266274\approx0.2266` [using z-value table.]

Hence, the probability that the person's BMI is more than 25.5 = 0.2266