Question

A box sits on the back of a flatbed truck. If the coefficient of static friction between the box and the truck bed is μs = 0.400, what is the shortest distance in which the truck can stop on level ground without the box sliding if it is initially traveling at v = 15.0 m/s?

Answer 1

28,699m

Step-by-step explanation:

The force to make the box move should be μs.N=μs.m.g=m.|a|

then,

|a|=μs.g

Being

μs coefficient of static friction,

N the force made by the truck on the box caused by the gravity force,

m the mass,

g the acceleration of gravity

and a the acceleration of the truck.

`x = v * t + (1)/(2) * a * {t}^(2)`

as the truck is stopping, the acceleration is negative. then,

`x = v * t - (1)/(2) * |a| * {t}^(2)`

`|a| = v / t \\ t = v / |a|`

`x = v * (v / |a| ) - (1)/(2) * |a| * a^(2)`

`x = v * (v / μs.g ) - (1)/(2) * |a| * {(v / μs.g)}^(2)`

`x = \frac{{v}^(2)}{μs * g} - (1)/(2) * \frac{{v}^(2)}{μs * g} \\ x = (1)/(2) * \frac{{v}^(2)}{μs * g} \\ x = 0.5 * \frac{{(15m/s) }^(2) }{0.4 * 9.8m/ {s}^(2) } = 28.699m`

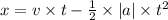
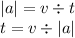
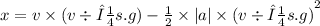
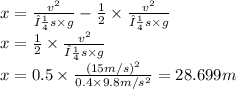
28,699m