Question

Block 1 (mass 2.00 kg) is moving rightward at 10.0 m/s and block 2 (mass 5.00 kg) is moving rightward at 3.00 m/s. The surface is frictionless, and a spring with a spring constant of 1120 N/m is fixed to block 2. When the blocks collide, the compression of the spring is maximum at the instant the blocks have the same velocity. (a) Find the maximum compression. (b) Find the final velocities of the two blocks.

Answer 1

Maximum compression= 0.25 m

Final velocities= 5 m/s

Step-by-step explanation:

From the law of conservation of momentum

m1v1 + m2v2=(m1+m2)Vc where m1 is mass of block 1, m2 is mass of block 2, v1 is velocity of block 1, v2 is velocity of block 2, vc is the common velocity of the two blocks.

Substituting 2Kg for m1, 5kg for m2, 10m/s for v1, 3m/s for v2 we obtain

2Kg*10m/s + 5kg*3m/s=(2+5)Vc

7Vc=20+15

7Vc=35

Vc=35/7=5m/s

From law of conservation of energy

Final energy-Initial energy+Energy stored in spring=0

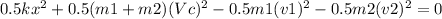`0.5kx^(2)+0.5(m1+m2)(Vc)^(2)-0.5m1(v1)^(2)-0.5m2(v2)^(2)=0` where x represent compression of spring

`0.5*1120x^(2)+0.5(2+5)*5^(2)-0.5(2*10^(2))-0.5(5*3^(2))=0`

`560x^(2)+87.5-100-22.5=0`

`560x^(2)-35=0`

`560x^(2)=35`

`X^(2)=35/560=0.0625`

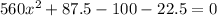
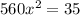
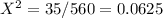
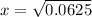`x=\sqrt {0.0625}`=0.25 m