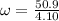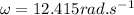Answer: [tex]12.415 rad.s^{-1}[/tex]
Explanation: Angular velocity is the rate of change in angular displacement.
We know that:
Angular velocity,
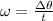 ....................(1)
....................(1)
where:
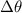 = angular displacement in radians
= angular displacement in radians
Given that:
Putting the respective values in eq. (1)