Question

In a game of pool, the cue ball strikes another ball of the same mass and initially at rest. After the collision, the cue ball moves at 4.60 m/s along a line making an angle of 28.0° with its original direction of motion, and the second ball has a speed of 3.40 m/s. Find (a) the angle between the direction of motion of the second ball and the original direction of motion of the cue ball and (b) the original speed of the cue ball.

Answer 1

(a)
`-39.4^(\circ)`

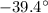
Let's take the initial direction (before the collision) of the cue ball has positive x-direction.

Along the y-direction, the total initial momentum is zero:

`p_y =0`

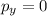
Therefore, since the total momentum must be conserved, it must be zero also after the collision. So we write:

`0 = m v_1 sin \phi_1 + m v_2 sin \phi_2 \\0 = m(4.60) sin (28^(\circ)) + m(3.40) sin \phi_2`

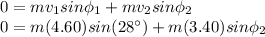
where

m is the mass of each ball

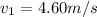`v_1= 4.60 m/s` is the velocity of the cue ball after the collision

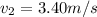`v_2 = 3.40 m/s` is the velocity of the second ball after the collision

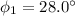`\phi_1=28.0^(\circ)` is the angle of the cue ball with the x-axis

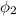`\phi_2` is the angle of the second ball

Solving for
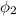`\phi_2`, we find the angle between the direction of motion of the second ball and the original direction of motion:

`sin \phi_2 = -(4.60 sin 28)/(3.40)=-0.635\\\phi_2 = -39.4^(\circ)`

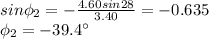
(b) 6.69 m/s

To find the original speed of the cue ball, we analyze the situation along the horizontal direction.

First, we calculate the total momentum along the x-direction after the collision, which is:

`p_x = m v_1 cos \phi_1 + m v_2 cos \phi_2 \\0 = m(4.60) cos (28^(\circ)) + m(3.40) cos (-39.4^(\circ))=6.69 m`

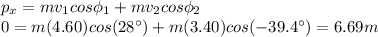
The initial total momentum along the x-direction as

`p_x = m u`

where

m is the mass of the cue ball

`u` is the initial velocity of the cue ball

The momentum along this direction must be conserved, so we can equate the two expressions and find the value of u:

`mu = 6.69 m\\u = 6.69 m/s`