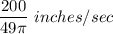Answer: The height of the oil changing at the rate of
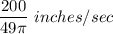
Explanation:
Since we have given that
volume is increasing at a rate of 150 cubic inches per second.
Height of cylinder = 10 times of radius.
As we know the formula for "Volume":
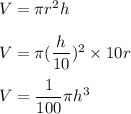
We will derivative it w.r.t 't'.
So, it becomes,

Hence, the height of the oil changing at the rate of