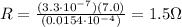Answer:
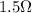
Step-by-step explanation:
The resistance of a piece of wire is given by
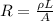
where
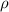 is the resistivity of the material
is the resistivity of the material
L is the length of the wire
A is the cross-sectional area
In this problem, we have
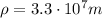
L = 7.0 m
The diameter of the wire is 0.14 cm, so the radius is 0.07 cm, therefore the cross sectional area is
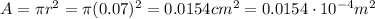
Therefore, the resistance is