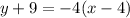Answer:
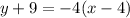
Explanation:
Linear equations can take various forms, such as:
- Point–slope form
- Two-point form
- Slope–intercept form
- Intercept form
- Standard form
The point-slope form of a linear equation is written as:

Where:
So, according to the data provided:
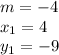
Replacing the data into the point-slope equation:
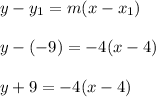
Therefore, the equation for the graph shown is: