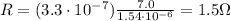Question

Taking the resistivity of platinoid as 3.3 x 10-7 m, find the resistance of 7.0 m of platinoid wire of average diameter 0.14 cm.

Answer 1

`1.5 \Omega`

Step-by-step explanation:

The resistance of a wire is given by the equation:

`R=\rho (L)/(A)`

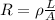
where

`\rho` is the resistivity of the material

L is the length of the wire

A is the cross-sectional area of the wire

In this problem, we have a wire of platinoid, whose resistivity is

`\rho = 3.3\cdot 10^(-7) \Omega m`

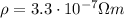
The length of the wire is

L = 7.0 m

And its radius is

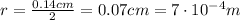`r=(0.14 cm)/(2)=0.07 cm = 7\cdot 10^(-4) m`, so the cross-sectional area is

`A=\pi r^2=\pi(7\cdot 10^(-4))^2=1.54\cdot 10^(-6)m^2`

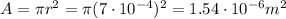
Solving for R, we find the resistance of the wire:

`R=(3.3\cdot 10^(-7))(7.0)/(1.54\cdot 10^(-6))=1.5 \Omega`