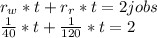Question

Wilma can mow a lawn in 40 minutes. Rocky can mow the same lawn in 120 minutes. Construct an equation that would allow you to determine how long it would take them to mow 2 lawns if they worked together. Use t to represent the number of minutes they work.

Answer 1

`r_(w)*t + r_(r)*t = 2 jobs\\ (1)/(40) *t + (1)/(120) *t = 2`

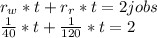
Explanation:

Given are the time it takes for each worker (Wilma and Rocky) to mow one lawn.

To derive a formula to be able to find the time it takes if they work together we first need to find the rate of work of each worker

The basic formula for rate of working is as follow

`rate(r) = (Job)/(time)`

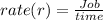
Lets calculate the rate of work for Wilma and Rocky

Wilma

`r_(w) = (1)/(40)`

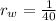
Rocky

`r_(r) = (1)/(120)`

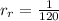
Notice the 1 at the numerator, this is because the times are given for one job.

To complete two jobs together we derive the following formula based on adding their rates together

`r_(w)*t + r_(r)*t = 2 jobs\\ (1)/(40) *t + (1)/(120) *t = 2`