Question

17 copper wires of length l and diameter d are connected in parallel to form a single composite conductor of resistance R. What is the ratio of the diameter of a single copper wire to d, if its length is also l and it has the same resistance?

Answer 1

`(D)/(d) = 4.12`

Step-by-step explanation:

As we know that resistance of one copper wire is given as

`r = \rho (L)/(a)`

here we know that

`a = \pi ((d)/(2))^2`

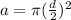
now we have

`r = \rho (L)/(\pi ((d^2)/(4)))`

`r = \rho (4L)/(\pi d^2)`

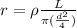
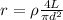
now we know that such 17 resistors are connected in parallel so we have

`R = (r)/(17)`

`R = \rho (4L)/(17 \pi d^2)`

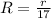
Now if a single copper wire has same resistance then its diameter is D and it is given as

`R = \rho (4L)/(\pi D^2)`

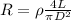
now from above two equations we have

`\rho (4L)/(\pi D^2) = \rho (4L)/(17 \pi d^2)`

`D^2 = 17 d^2`

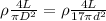
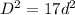
now we have

`(D)/(d) = 4.12`