Question

There are two machines available for cutting corks intended for use in wine bottles. Measurements of 25 corks from the first machine indicates that it produces corks with diameters that are distributed with a sample mean 2.99 cm and sample standard deviation 0.08 cm. Measurements of 30 corks from the second machine reveals that it produces corks with diameters that have a distribution with sample mean 3.04 cm and sample standard deviation 0.04 cm. Acceptable corks have diameters between 2.9 cm and 3.1 cm. 1) What is the uncertainty in the true mean cork diameter for the first machine?

2) What is the uncertainty in the true mean cork diameter for the second machine?
3) What is the probability that the first machine will produce an acceptable cork? 4) What is the probability that the second machine will produce an acceptable cork? (Round your answer to four decimal places.)

Answer 1

1) 0.016

2) 0.0073

3) 78.51%

4) 93.3%

Explanation:

The standard uncertainty is defined as the standard error of the mean

`\bf SEM=(s)/(√(n))`

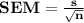
where

s = sample standard deviation

n = sample size

1)

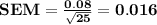
`\bf SEM=(0.08)/(√(25))=0.016`

2)

`\bf SEM=(0.04)/(√(30))=0.0073`

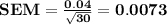
3)

Given that acceptable corks have diameters between 2.9 cm and 3.1 cm, the probability that the first machine will produce an acceptable cork is the area between 2.9 and 3.1 of the Normal curve of mean 2.99 and standard deviation 0.08.

This area can be calculated easily with a spreadsheet and we obtain a probability of 0.7851 or 78.51%

4)

The probability is the area between 2.9 and 3.1 of the Normal curve of mean 3.04 and standard deviation 0.04 which is 0.933 or 93.3%