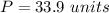Answer:
Explanation:
we know that
The perimeter of a rectangle is equal to
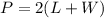
where
L is the length of rectangle
W is the width of rectangle
Let
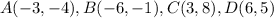
Remember that
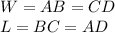
the formula to calculate the distance between two points is equal to
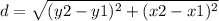
step 1
Find the distance AB
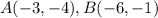
substitute in the formula
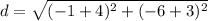
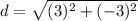
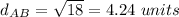
step 2
Find the distance BC
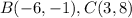
substitute in the formula
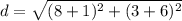
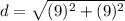
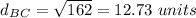
step 3
Find the perimeter
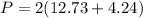
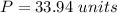
Round to the nearest tenth