Question

(I think I know it just checking) Which function has a period equal to half the period of the function in y=5cos(3/5x-pi)+4.. the period is 10pi/3

I think its the first one.

1. y=5sin(6/5x-pi)-4
2. y=-5/2sin(6/10x-2pi)+1/2
3. y=-4cos(5/6x-2pi)+5
4. y=2cos(3/10x-pi)-5/2

Answer 1

A is your answer

Explanation:

Answer 2

`y=5sin((6)/(5)x- \pi )-4`

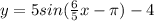
Explanation:

The given function is

`y=5cos((3)/(5)x- \pi )+4`

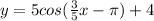
Where
`T=(10 \pi)/(3)`

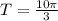
Notice half the period is

`(T)/(2)=((10 \pi)/(3) )/(2)=(10 \pi)/(6)=(5 \pi)/(3)`

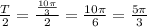
Now, in the first function

`y=5sin((6)/(5)x- \pi )-4`

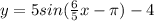
Notice that this function is in the form:
`y=Asin(\omega x + \phi)`

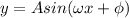
Where
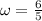`\omega =(6)/(5)`, which definition is
`\omega = (2 \pi)/(T)`

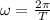
Replacing this value, we have

`(6)/(5)=(2 \pi)/(T)\\ T=(10 \pi)/(6)\\ T=(5 \pi)/(3)`

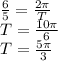
Which means the first function is has half the period of the given function.