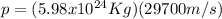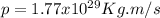Answer:
(a)
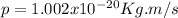
(b)

(c)
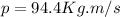
(d)
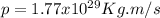
Step-by-step explanation:
The linear momentum is defined as:
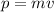 (1)
(1)
Where m is the mass and v is the velocity
a.) A proton with mass
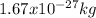 moving with a velocity of
moving with a velocity of
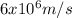 .
.
Replacing those values in equation (1) it is gotten:
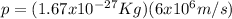
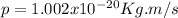
So, it has a linear momentum of
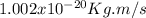
b.) A 1.6 g bullet moving with a speed of 374m/s to the right.
Notice that in this case it is necessary to express the mass of the bullet in terms of kilograms:
 ⇒
⇒
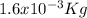
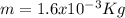
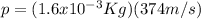

c.) A 8 kg sprinter running with a velocity of 11.8 m/s.
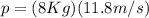
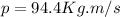
d.) Earth (
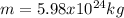 ) moving with an orbital speed equal to 29700 m/s.
) moving with an orbital speed equal to 29700 m/s.