Question

A child pulls a 3.00-kg sled across level ground at constant velocity with a light rope that makes an angle 30.0° above horizontal. The tension in the rope is 5.00 N. Assuming the acceleration of gravity is 9.81 m/s2, what is the coefficient of friction between the sled and the ground?

Answer 1

μ = 0.161

Step-by-step explanation:

Since the tension on the rope (F) is being applied at an angle (θ), it should be decomposed into a vertical and a horizontal component.

The vertical component of the tension on the rope (F*sin(θ)) is pulling the sled upwards, decreasing the normal force.

Therefore, the normal force can be calculated as:

`N = m*g - F*sin(\theta)\\N= 3*9.8 - 5*sin(30)\\N= 26.9 N`

The horizontal component of the tension on the rope (F*cos(θ)) is the force being applied to move the sled and that should equal the coefficient of friction multiplied by the normal force.

`F*cos(\theta)=N*\mu\\5*cos(30)=26.9*\mu\\\mu=0.161`

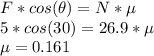
the coefficient of friction between the sled and the ground is 0.161