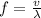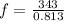Question

Two in-phase loudspeakers that emit sound with the same frequency are placed along a wall and are separated by a distance of 5.00 m. A person is standing 12.0 m away from the wall, equidistant from the loudspeakers. When the person moves 1.00 m parallel to the wall, she experiences destructive interference for the first time. What is the frequency of the sound? The speed of sound in air is 343 m/s.

Answer 1

`f = 421.8 Hz`

Step-by-step explanation:

When she moved a distance of 1 m from mid point she observe first destructive interference due to two speakers

so we can say that path difference of sound due to two speakers will be equal to half of the wavelength

so path difference is given as

`\Delta L = {3.5^2 + 12^2}^(0.5) - {1.5^2 + 12^2}^(0.5)`

so it will be

`\Delta L = 12.5 - 12.093`

`\Delta L = 0.4066`

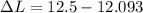
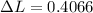
now we know that

`(\lambda)/(2) = 0.4066`

`\lambda = 0.813`

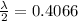
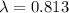
now frequency of sound is given as

`f = (v)/(\lambda)`

`f = (343)/(0.813)`

`f = 421.8 Hz`