Answer:
The maximum number of toys you can afford to buy is 40
Explanation:
Let
x -----> the number of toys
we have the compound inequality

Divide into two inequalities
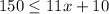 -----> inequality A
-----> inequality A
 ----> inequality B
----> inequality B
Solve the inequality A
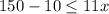
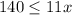
Divide by 11 both sides
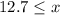
Rewrite
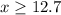
Solve the inequality B
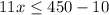
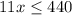
Divide by 11 both sides

The solution for x is the interval ----> [13,40}
Remember that the number of toys must be a whole number
The domain is all whole numbers greater than or equal to 13 toys and less than or equal to 40 toys
therefore
The maximum number of toys you can afford to buy is 40