Answer:
0.42 is closest to the proportion of customer purchase amounts between $14.00 and $16.00
Explanation:
Mean =
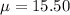
Standard deviation =
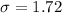
We are supposed to find the proportion of customer purchase amounts between $14.00 and $16.00
P(14<x<16)
Formula :

At x = 14
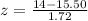
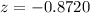
Refer the z table for p value
P(x<14)=0.1922
At x = 16

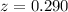
Refer the z table for p value
P(x<16)=0.6141
P(14<x<16)=P(x<16)-P(x<14)=0.6141-0.1922=0.42
So, Option C is true
Hence 0.42 is closest to the proportion of customer purchase amounts between $14.00 and $16.00