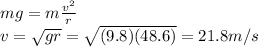Question

A motorcycle is traveling up one side of a hill and down the other side. The crest of the hill is a circular arc with a radius of 48.6 m. Determine the maximum speed that the cycle can have while moving over the crest without losing contact with the road.

Answer 1

The maximum speed a motorcycle can have while moving over the crest of a hill with a radius of 48.6 m without losing contact with the road is approximately 21.83 m/s. This is calculated using the centripetal force equation set equal to gravitational force.

Step-by-step explanation:

The question is asking to determine the maximum speed a motorcycle can have while moving over the crest of a hill without losing contact with the road, given that the crest is a circular arc with a radius of 48.6 m. To calculate this, we use the concept of circular motion and the fact that the maximum speed will be achieved when the normal force becomes zero, which is the condition for the motorcycle just losing contact with the road. At this point, the gravitational force provides the required centripetal force for circular motion.

We set the centripetal force (mv2/r) equal to the gravitational force acting on the motorcycle (mg), where m is the mass of the motorcycle, v is its velocity, and r is the radius of the circular arc. Therefore, we have mv2/r = mg, which simplifies to v2 = rg. After canceling out 'm' and taking the square root, we obtain v = √(rg). Given that g is approximately 9.81 m/s2, we can substitute the values to find the maximum speed:

v = √(48.6 m × 9.81 m/s2) = √(476.586) ≈ 21.83 m/s

Therefore, the maximum speed that the motorcycle can have while moving over the crest without losing contact with the road is approximately 21.83 m/s.

Answer 2

21.8 m/s

Step-by-step explanation:

At the top of the hill (crest), there are two forces acting on the motorcycle:

- The reaction force of the road, N (upward)

- The force of gravity, mg (downward)

Since the motorcycle is moving by circular motion, the resultant of these forces will give the centripetal force, so:

`mg-N = m(v^2)/(r)`

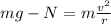
where the direction of the weight (mg) is equal to that of the centripetal force, and where

m is the mass of the cycle

g = 9.8 m/s^2 is the acceleration of gravity

v is the speed

r = 48.6 is the radius of the hill

The cycle loses contact with the road when the reaction force becomes zero:

N = 0

Substituting into the equation, we therefore find the maximum speed that is allowed for the cycle before losing constact:

`mg = m(v^2)/(r)\\v=√(gr)=√((9.8)(48.6))=21.8 m/s`