Question

Two planets are observed going around a star. Planet xoron has an orbital period that is twice as long as planet krypton. Which planet has a shorter average orbital radius?

Answer 1

Krypton

Step-by-step explanation:

Kepler's third law states that the cube of the semimajor axis of the orbit of a planet is proportional to the square of the orbital period. Mathematically, we can write:

`(r^3)/(T^2)=const.`

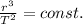
or

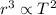`r^3 \propto T^2` (1)

where

r is the semimajor axis of the orbit

T is the orbital period

In this problem, we are told that Planet xoron has an orbital period twice as long as planet kripton: given relationship (1), this means that Planet xoron will also have a longer orbital radius (so, planet krypton has a shorter orbital radius).

Mathematically, we can write the equation as

`(r_x^3)/(T_x^2)=(r_k^3)/(T_k^2)`

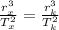
where 'x' stands for Xoron and 'k' stands for Krypton. Since

`T_x = 2 T_k`

The ratio between the radii will be

`(r_x^3)/(r_k^3)=(T_x^3)/(T_k^2)=((2T_k)^2)/(T_k^2)=4`

So, Krypton will have a shorter average orbital radius.