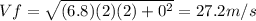Question

sing a rope that will snap if the tension in it exceeds 361 N, you need to lower a bundle of old roofing material weighing 455 N from a point 6.80 m above the ground. (a) What magnitude of the bundle's acceleration will put the rope on the verge of snapping? (b) At that acceleration, with what speed would the bundle hit the ground

Answer 1

a)-2m/s^2

b)27.2m/s

Step-by-step explanation:

Hello! The first step to solve this problem is to find the mass of the block remembering that the definition of weight force is mass by gravity (g=9.8m / s ^ 2)

W=455N=weight

W=mg

W=455N=weight

`m=(W)/(g) =(455)/(9.81)=46.38kg`

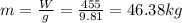
The second step is to draw the free body diagram of the body (see attached image) and use Newton's second law that states that the sum of the forces is equal to mass by acceleration

`a=(T-W)/(m) =(361-455)/(46.38kg) =-2m/s^2`

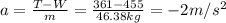
for point b we use the equations of motion with constant acceleration to find the velocity

`Vf=√(X(2)(a)+Vo^2)`

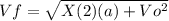
Where

Vf = final speed

Vo = Initial speed =0

A = acceleration =2m/s

X = displacement =6.8m

Solving

`Vf=√((6.8)(2)(2)+0^2)=27.2m/s`