Question

The driver of a car going 96.0 km/h suddenly sees the lights of a barrier 39.0 m ahead. It takes the driver 0.75 s to apply the brakes, and the average acceleration during braking is -10.0 m/s2. (b) What is the maximum speed at which the car could be moving and not hit the barrier 39.0 m ahead?

Answer 1

21.42m/S

Step-by-step explanation:

Hello!

To solve this problem we must perform the following steps.

1. Find the distance traveled from until the driver reacts, this is achieved using the equation for constant speed movement.

X1=VT

where

x= distance traveled

v=initial speed

T=time=0.75s

X1=0.75Vo

we must take into account that the total distance is the sum of the distance at which the pilot reacts (x1) and when it starts to decelerate (x2)

39=0.75Vo+X2

X2=39-0.75Vo

2. Now we use the equation that defines a movement with constant acceleration.

`Vo =√(Vf^2 - 2(a)(x2))`

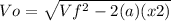
where

Vf = final speed=0m/s

Vo = Initial speed

A = acceleration =-10m/s2

X2 = displacement

now we use the ecuation of step 1

`Vo =√(Vf^2 - 2(a)(39-0.75Vo))`

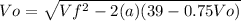
solving

`Vo =√(0 - 2(-10))(39-0.75Vo))\\Vo^2=780-15Vo\\Vo^2+15Vo-780=0`

Now we solve the quadratic equation and find the value of Vo

the solutions are 21.42m/S, -36.41m/S

as the speed must be positive we conclude that the answer is 21.42m/S