Question

A recent study reports that only 34% of Americans consume their daily recommended intake of fiber. A nutritionist takes a SRS of 45 individuals who come to her for a diet consultation and records whether or not each gets their daily recommended intake of fiber. She finds that 18 of out the 45 do, or 40%. What is the distribution of the sample proportion? p ~ N (0.40, 0.0732) p ~ N (0.40, 0.0712) p^^\^ ~ N (0.34, 0.0712) p^^\^ ~ N (0.34, 0.0732) The sample size is too small to say what the distribution of the sample proportion is.

Answer 1

The distribution of the sample proportion ~ N(0.4, 0.07302)

Explanation:

The distribution of the data can be modeled with a binomial distribution with probability p = 0.4 of finding a person that consume her or his daily recommended intake of fiber, and q = 0.6

If n is the sample size, we must check if np ≥ 10 and nq ≥ 10, so we can approximate the Binomial with a Normal distribution.

The sample size is 45

45*0.4 = 18 > 10 and 45*0.6 = 27 > 10.

The distribution of the sample proportion ~ the Normal with mean p and standard deviation

`\bf \sqrt{(pq)/(n)}=\sqrt{(0.4*0.6)/(45)}=0.07302`

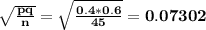
and

The distribution of the sample proportion ~ N(0.4, 0.07302)