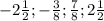Question

Drag and drop each number to its correct position on the number line. (-3/8) (7/8) (-2 1/2) (2 1/2) Please answer quickly !!

Answer 1

`-2(1)/(2);-(3)/(8);(7)/(8);2(1)/(2)`

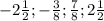
Explanation:

Here we need to order all numbers from least to greatest. To do that, we can recur to the decimal number of each fraction.

We have
`-(3)/(8);(7)/(8);-2  (1)/(2) ;2(1)/(2)`

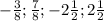
First, we have to position the negative numbers, because they are less than positive numbers. Between
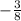`-(3)/(8)` and -2 \frac{1}{2}, which is the least?

`-(3)/(8) =-0.375`

`-2(1)/(2) =-2.5`

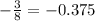
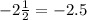
Therefore, we have to position
`-2(1)/(2)` first, second
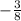`-(3)/(8)`, because -2.5 is less than -0.375.

To position the other two numbers we do the same process:

`2(1)/(2) =2.5`

`(7)/(8)=0.875`

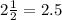
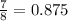
In this case, 2.5 is more than 0.875. So, the fourth number is 0.875 and the fifth number is 2.5.

Therefore, the correct position is:

`-2(1)/(2);-(3)/(8);(7)/(8);2(1)/(2)`